本文最后更新于 2025-10-23,文章内容可能已经过时。
一、行列式
在求解二元一次方程组时,如 \displaystyle \left\{ \begin{aligned} x + 2y = 5 \\ 3x + 4y = 6 \end{aligned} \right.,我们可以进行如下处理:
\begin{aligned}
(x + 2y) \times 3 - (3x + 4y) = 5 \times 3 - 6
\end{aligned}
解得:
\left\{
\begin{aligned}
x &= -4 \\
y &= \frac{9}{2}
\end{aligned}
\right.
而如果我们设关于 x_1, x_2 的方程组 \displaystyle \left\{ \begin{aligned} a_{11}x + a_{12}y = b_1 \\ a_{21}x + a_{22}y = b_2 \end{aligned} \right.,则方程的解可以转化为以下形式:
\left\{
\begin{aligned}
x_1 &= \frac{b_1a_{22} - b_2a_{12}}{a_{11}a_{22} - a_{12}a_{21}} \\
x_2 &= \frac{b_2a_{11} - b_1a_{21}}{a_{11}a_{22} - a_{12}a_{21}}
\end{aligned}
\right.
而这一长串看着眼花,记着也没啥必要。并且如果扩展到 n 元方程组,那么式子会更加复杂。
为了简化记忆与方便计算,因此引入了行列式。
1. 定义
对于 n 阶行列式,是由 n^2 个数字组成的一个 n \times n 大小的方阵,即:
D =
\left\vert
\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\cdots & \cdots & \cdots & \cdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{array}
\right\vert
关于行列式的定义实际就这么多,没了(除了计算值的部分)。
2. 行列式的值
在计算它的值之前,我们先引入一个概念:逆序数。
对于一个排列(序列)A = (a_1, a_2, \cdots, a_n),如果存在两个下标为 i 和 j 的数字,满足以下两个条件:
- 下标顺序:i < j
- 数值大小:a_i > a_j
那么,(a_i, a_j) 就被称为该排列(又可以叫做序列/数列,反正哪个好理解就叫哪个)中的一个逆序对。
简单来说,一个逆序对就是指序列中前面的元素大于后面的元素的任意一对元素。
例如:一个排列 A = (2, 4, 1, 3),我们可以发现的逆序对有:(2, 1)、(4, 1)、(4, 3)。因此这个排列的逆序对总数(即逆序数)为 3。
由此,我们设一个 n 级排列为 j_1j_2 \cdots j_n,那么该排列的逆序数表示为 \tau(j_1j_2 \cdots j_n)。
因此对于上述例子的排列,我们可以表示为:\tau(2413) = 3。
根据逆序数的定义,我们可以发现,n 级排列逆序数的范围为:\displaystyle [0, \frac{n(n - 1)}{2}]。
接下来回到行列式中,那逆序数和行列式有什么关系呢?
我们设 j_1j_2 \cdots j_n 为 1 \sim n 的全排列,则 \tau(j_1j_2 \cdots j_n) 为它的逆序数。(此时固定行标的排列为 1 \sim n 便于计算,实际可以不固定,即使用 p, q 来表示行/列的 1 \sim n 排列)
对于 n 阶行列式,它的值为:
\begin{align*}
D =
\left\vert
\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\cdots & \cdots & \cdots & \cdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{array}
\right\vert
&= \sum (-1)^{\tau(j_1j_2 \cdots j_n)}a_{1j_1}a_{2j_2} \cdots a_{nj_n} \\
&= \sum (-1)^{\tau(p_1p_2\cdots p_n) + \tau(q_1q_2\cdots q_n)}a_{p_1q_1}a_{p_2q_2} \cdots a_{p_nq_n}
\end{align*}
由此定义,我们可以发现它的项数有 n! 项(因为 n 个数的全排列就是 n! 嘛),且每一项都是从每一行中选一个数相乘。
从定义可以看出,对于行列式计算中的项:
- 如果逆序数的值为奇数(奇排列),则前面的符号为 -;
- 如果逆序数的值为偶数(偶排列),则前面的符号为 +。
如果将一个排列中任意两个位置不相同的元素进行交换,那么逆序数的奇偶性一定发生改变。
3. 对角线法则
tips:info
关于对角线法则,实际上仅适用于二、三阶的行列式,对于四阶及以上阶数的行列式并不通用。
对于四阶行列式,使用定义可知一共有 24 项;但是套用对角线法则,则只有 8 项。
对于四阶及以上阶数的行列式,可以降维到二、三阶,再套用对角线法则即可。
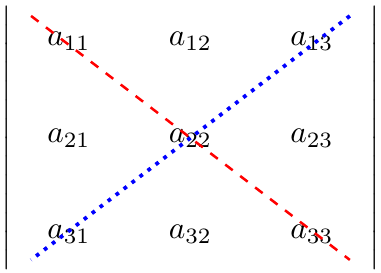
我们通常将红色的线叫做主对角线,蓝色的线叫做副对角线。
对于二阶行列式有:
D =
\left\vert
\begin{array}{cc}
a & b \\
c & d
\end{array}
\right\vert
= ad - cb
详细如下图所示,即主对角线上的数相乘减去副对角线上的数相乘。
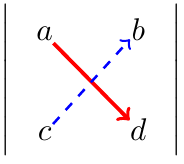
对于三阶行列式有:
\begin{align*}
D =
\left\vert
\begin{array}{cccc}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}
\right\vert
&= a_{1\textcolor{red}1}a_{2\textcolor{red}2}a_{3\textcolor{red}3} + a_{1\textcolor{red}2}a_{2\textcolor{red}3}a_{3\textcolor{red}1} + a_{1\textcolor{red}3}a_{2\textcolor{red}1}a_{3\textcolor{red}2} \\
&- (a_{1\textcolor{blue}3}a_{2\textcolor{blue}2}a_{3\textcolor{blue}1} + a_{1\textcolor{blue}1}a_{2\textcolor{blue}3}a_{3\textcolor{blue}2} + a_{1\textcolor{blue}2}a_{2\textcolor{blue}1}a_{3\textcolor{blue}3})
\end{align*}
详细如下图所示,即主对角线上的数相乘并相加,减去副对角线上的数相乘。
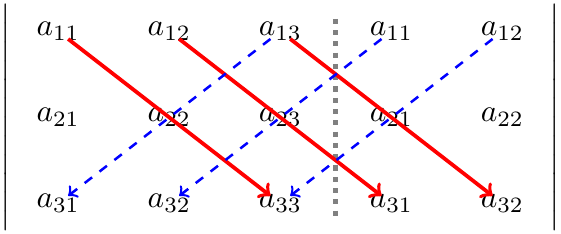
4. 行列式的性质
行列式的转置操作会将行列式沿主对角线进行镜像翻转。
性质1:行列式转置,行列式的值不变。
\begin{align*}
\vert D \vert=
\left\vert
\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{array}
\right\vert
=
\left\vert
\begin{array}{cccc}
a_{11} & a_{21} & \cdots & a_{n1} \\
a_{12} & a_{22} & \cdots & a_{n2} \\
\vdots & \vdots & \ddots & \vdots \\
a_{1n} & a_{2n} & \cdots & a_{nn}
\end{array}
\right\vert
= \vert D^T \vert
\end{align*}
性质2:行列式交换两行(列),其值反号。
\begin{align*}
\left\vert
\begin{array}{cccc}
\cdots & \cdots & \cdots & \cdots \\
a_{i1} & a_{i2} & \cdots & a_{in} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{array}
\right\vert
= -
\left\vert
\begin{array}{cccc}
\cdots & \cdots & \cdots & \cdots \\
a_{n1} & a_{n2} & \cdots & a_{nn} \\
\vdots & \vdots & \ddots & \vdots \\
a_{i1} & a_{i2} & \cdots & a_{in}
\end{array}
\right\vert
\end{align*}
性质3:行列式某行(列)乘 k,等价于 k 乘原行列式。
\begin{align*}
\left\vert
\begin{array}{cccc}
\cdots & \cdots & \cdots & \cdots \\
k \cdot a_{i1} & k \cdot a_{i2} & \cdots & k \cdot a_{in} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{array}
\right\vert
= k
\left\vert
\begin{array}{cccc}
\cdots & \cdots & \cdots & \cdots \\
a_{n1} & a_{n2} & \cdots & a_{nn} \\
\vdots & \vdots & \ddots & \vdots \\
a_{i1} & a_{i2} & \cdots & a_{in}
\end{array}
\right\vert
\end{align*}
性质4:行列式某行(列)元素均为两个数之和,则行列式可以分解为两个行列式之和。(一次只能拆一行)
\begin{align*}
\left\vert
\begin{array}{cccc}
\cdots & \cdots & \cdots & \cdots \\
\textcolor{red}{a_{i1}} + \textcolor{blue}{b_{i1}} & \textcolor{red}{a_{i2}} + \textcolor{blue}{b_{i2}} & \cdots & \textcolor{red}{a_{in}} + \textcolor{blue}{b_{in}} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{array}
\right\vert
=
\left\vert
\begin{array}{cccc}
\cdots & \cdots & \cdots & \cdots \\
\textcolor{red}{a_{n1}} & \textcolor{red}{a_{n2}} & \cdots & \textcolor{red}{a_{nn}} \\
\vdots & \vdots & \ddots & \vdots \\
a_{i1} & a_{i2} & \cdots & a_{in}
\end{array}
\right\vert
+
\left\vert
\begin{array}{cccc}
\cdots & \cdots & \cdots & \cdots \\
\textcolor{blue}{b_{n1}} & \textcolor{blue}{b_{n2}} & \cdots & \textcolor{blue}{b_{nn}} \\
\vdots & \vdots & \ddots & \vdots \\
a_{i1} & a_{i2} & \cdots & a_{in}
\end{array}
\right\vert
\end{align*}
性质5:将行列式的某行(列)元素的 k 倍加到另一行(列)上,行列式的值不变。(可以将行列式转化为上三角或下三角,简化计算)
\begin{align*}
\left\vert
\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{array}
\right\vert
=
\left\vert
\begin{array}{cccc}
a_{11} + k \cdot a_{n1} & a_{12} + k \cdot a_{n2} & \cdots & a_{1n} + k \cdot a_{nn} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{array}
\right\vert
\end{align*}
5. 行列式的计算
对于四阶及以上的行列式,我们可以发现对角线法则不生效了,那我们只能按照定义一步一步去算吗?
我们知道,行列式的阶越低越容易计算,于是很自然地提出,能否把高阶行列式转换为低阶行列式来计算,为此,引入了余子式和代数余子式。
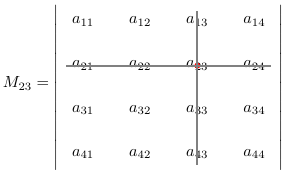
余子式(M_{ij}):设 \vert A \vert 是一个 n 阶行列式,划去第 i 行和第 j 列,剩下的 (n-1)^2 个元素按照原来的顺序组成了一个 n-1 阶的行列式,这个行列式称为 \vert A \vert 的第 (i, j) 元素的余子式,记为 M_{ij}.
代数余子式:前面带着符号的余子式为代数余子式,记为:
A_{ij} = (-1)^{i + j} M_{ij}
\begin{align*}
A_{23} =
\left\vert
\begin{array}{ccc}
a_{11} & a_{12} & a_{14} \\
a_{31} & a_{32} & a_{34} \\
a_{41} & a_{42} & a_{44}
\end{array}
\right\vert
\end{align*}
拉普拉斯定理:
对于一个 n 阶行列式,可以将其按照某一行进行展开:
\begin{align*}
D_n =
\left\vert
\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{array}
\right\vert
&= a_{i1}A_{i1} + a_{i2}A_{i2} + \cdots + a_{in}A_{in} & (按行展开)\\
&= a_{1j}A_{1j} + a_{2j}A_{2j} + \cdots + a_{nj}A_{nj} & (按列展开)
\end{align*}
特别地,对于下列行列式的形式:
\begin{align*}
D =
\left\vert
\begin{array}{c}
a_{11} & \cdots & a_{1k} & & & \\
\vdots & \ddots & \vdots & & O & \\
a_{k1} & \cdots & a_{kk} & & & \\
c_{11} & \cdots & c_{1k} & b_{11} & \cdots & b_{1n} \\
\vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\
c_{n1} & \cdots & c_{nk} & b_{n1} & \cdots & b_{nn}
\end{array}
\right\vert
=
\left\vert
\begin{array}{c}
p_{11} & & & & & \\
\vdots & \ddots & & & O & \\
p_{k1} & \cdots & p_{kk} & & & \\
c_{11} & \cdots & c_{1k} & q_{11} & & \\
\vdots & \ddots & \vdots & \vdots & \ddots & \\
c_{n1} & \cdots & c_{nk} & q_{n1} & \cdots & q_{nn}
\end{array}
\right\vert
=
\left\vert
\begin{array}{c}
D_1 & O \\
C & D_2
\end{array}
\right\vert
= D_1D_2
\end{align*}
展开定理的逆运用:
\begin{align*}
D =
\left\vert
\begin{array}{c}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}
\right\vert
\Rightarrow
D^{\prime} =
\left\vert
\begin{array}{c}
1 & * & * & * \\
0 & a_{11} & a_{12} & a_{13} \\
0 & a_{21} & a_{22} & a_{23} \\
0 & a_{31} & a_{32} & a_{33}
\end{array}
\right\vert
=
\left\vert
\begin{array}{c}
1 & 0 & 0 & 0 \\
* & a_{11} & a_{12} & a_{13} \\
* & a_{21} & a_{22} & a_{23} \\
* & a_{31} & a_{32} & a_{33}
\end{array}
\right\vert
\end{align*}
那么这个逆运用有什么用呢?难不成只是为了升维?倒也不尽然。
好处是运用该方法之后,值与原来的值相同,即 D = D^{\prime}。并且,其最大的作用是带来了一个全是 * 的行(列),而这里则可以填写任意数字。
二、矩阵
矩阵 (Matrix) 是高等代数学中的一个基本概念,它是数学和工程学中用来表示数据和线性变换的重要工具。最早来自于方程组的系数及常数组成的方程。
1. 定义
对于一个线性方程组:
\begin{align*}
\left\{
\begin{array}{c}
7x_1 + 8x_2 + 9x_3 = 13 \\
4x_1 + 5x_2 + 6x_3 = 12 \\
x_1 + 2x_2 + 3x_3 = 11
\end{array}
\right.
\end{align*}
我们将 x_1, x_2, x_3 前面的系数,以及常数项抽离出来,写成矩阵的形式如下:
\begin{align*}
\left(
\begin{array}{c}
7 & 8 & 9 & 13 \\
4 & 5 & 6 & 12 \\
1 & 2 & 3 & 11
\end{array}
\right)
\end{align*}
由 m \times n 个数组成的一个 m 行 n 列的数表,就可以是一个矩阵。
\begin{align*}
A =
\left(
\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \cdots & a_{mn}
\end{array}
\right)_{m \times n}
\end{align*}
=
(a_{ij})_{m \times n}
同型矩阵:矩阵 A 的行数与列数与矩阵 B 的行数与列数相等,则称这两个矩阵为同型矩阵。
几个特殊类型的矩阵:
列矩阵:只有一列的矩阵,又称为列向量。
\begin{align*}
A =
\left(
\begin{array}{c}
a \\
b \\
c
\end{array}
\right)
\end{align*}
行矩阵:只有一行的矩阵,又称为行向量。
A =
\begin{array}{c}
(a & b & c)
\end{array}
零矩阵:矩阵内元素均为 0 的矩阵,记作 O。
O =
\left(
\begin{array}{c}
0 & 0 & 0 \\
0 & 0 & 0
\end{array}
\right)
方阵:行数与列数相等的矩阵。
单位矩阵:仅有主对角线上的元素为 1,其他位置上的元素均为 0 的方阵,记作 E。任何矩阵乘以单位矩阵均为任何矩阵。
方阵的行列式:对于一个方阵,其行列式的形式如下:
\begin{align*}
A =
\left(
\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{array}
\right)
\Rightarrow
\vert A \vert =
\left\vert
\begin{array}{cccc}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{array}
\right\vert
\end{align*}
2. 矩阵的运算
一个常数与矩阵相乘时,相当于矩阵内所有数同时乘上这个常数。
\begin{align*}
\lambda A =
\left(
\begin{array}{cccc}
\lambda a_{11} & \lambda a_{12} & \cdots & \lambda a_{1n} \\
\lambda a_{21} & \lambda a_{22} & \cdots & \lambda a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
\lambda a_{m1} & \lambda a_{m2} & \cdots & \lambda a_{mn}
\end{array}
\right)_{m \times n}
\end{align*}
两个同型矩阵相加时,对应位置的数相加。
\begin{align*}
A + B =
\left(
\begin{array}{cccc}
a_{11} + b_{11} & a_{12} + b_{12} & \cdots & a_{1n} + b_{1n} \\
a_{21} + b_{21} & a_{22} + b_{22} & \cdots & a_{2n} + b_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} + b_{m1} & a_{m2} + b_{m2} & \cdots & a_{mn} + b_{mn}
\end{array}
\right)_{m \times n}
\end{align*}
矩阵之间相乘时,仅当第一个矩阵 A 的列数与矩阵 B 的行数相等时才能定义,得到矩阵 C,即:
A_{m \times n} B_{n \times p} = C_{m \times p}
其中,矩阵 C 中的第 i 行第 j 列的元素为:
c_{ij} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots + a_{in}b_{nj} = \sum^n_{r = 1} a_{ir}b_{rj}
参考
- 逆序对 - 维基百科,自由的百科全书(wikipedia.org)
- 彻彻底底地理解行列式的定义,以及逆序数 - 知乎(zhihu.com)
- 行列式按行(列)展开(拉普拉斯定理) - 知乎(zhihu.com)
- 矩阵 - OI Wiki(io-wiki.org)
- 矩阵运算与常用矩阵 - 知乎(zhihu.com)







