本文最后更新于 2025-09-29，文章内容可能已经过时。

奇异值分解

线性代数相关知识

矩阵特征值和特征向量

定义

假设我们有一个 n 阶的矩阵 A 以及一个实数 \lambda，使得我们可以找到一个非零向量 \vec{x}，使得

A \vec{x} = \lambda \vec{x} \tag{1}

那么，我们称 \lambda 是矩阵 A 的一个特征值，而 \vec{x} 就是矩阵 A 的一个特征向量。

几何意义

对于一个 n 维的向量 \vec{x}，我们将它乘上一个 n 维的向量 A。得到的 A \vec{x} 实际上是对 \vec{x} 进行了一个线性变换，此时 \vec{x} 的长度和方向都发生了变化（一般情况下）。

但是对于特定的矩阵 A，总是存在一些特定方向的向量 \vec{x}，使得当 \vec{x} 乘以矩阵 A 时，\vec{x} 只有长度发生了变化。这个变化我们设为 \lambda 也就是矩阵 A 的一个特征值，而 \vec{x} 就是矩阵 A 的一个特征向量。

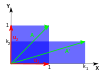
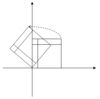
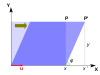
以下是矩阵 A 对于 \vec{x} 的常见线性变换的相关性质¹：

/	缩放	不等缩放	旋转	水平剪切	双曲线旋转
图例
A	\begin{bmatrix} k & 0 \\ 0 & k \end{bmatrix}	\begin{bmatrix} k_{1} & 0 \\ 0 & k_{2} \end{bmatrix}	\begin{bmatrix} \cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{bmatrix}	\begin{bmatrix} 1 & k \\ 0 & 1 \end{bmatrix}	\begin{bmatrix} \cosh{\varphi} & \sinh{\varphi} \\ \sinh{\varphi} & \cosh{\varphi} \end{bmatrix}
特征方程	(\lambda - k)^{2}	\begin{aligned} (\lambda - k_{1})(\lambda - k_{2}) \end{aligned}	\lambda^{2} - 2\cos(\theta)\lambda + 1	(\lambda - 1)^2	\lambda^{2} - 2\cosh(\varphi)\lambda + 1
特征值 \lambda_i	\begin{aligned} \lambda_1 = \lambda_2 = k \end{aligned}	\lambda_1 = k_1 \\ \lambda_2 = k_2	\begin{aligned} \lambda_1 & =e^{i \theta} \\ & =\cos \theta+i \sin \theta \\ \lambda_2 & =e^{-i \theta} \\ & =\cos \theta-i \sin \theta\end{aligned}	\begin{aligned} \lambda_1 = \lambda_2 = 1 \end{aligned}	\begin{aligned} \lambda_1 & =e^{\varphi} \\ & =\cosh \varphi+\sinh \varphi \\ \lambda_2 & =e^{-\varphi} \\ & =\cosh \varphi-\sinh \varphi\end{aligned}
代数重数\begin{aligned} \mu_i = \mu(\lambda_i) \end{aligned}	\mu_1 = 2	\mu_1 = 1 \\ \mu_2 = 1	\mu_1 = 1 \\ \mu_2 = 1	\mu_1 = 2	\mu_1 = 1 \\ \mu_2 = 1
几何重数\begin{aligned} \gamma_i = \gamma(\lambda_i) \end{aligned}	\gamma_1 = 2	\gamma_1 = 1 \\ \gamma_2 = 1	\gamma_1 = 1 \\ \gamma_2 = 1	\gamma_1 = 1	\gamma_1 = 1 \\ \gamma_2 = 1
特征向量	所有非零向量	\begin{aligned} & \mathbf{u}_1=\left[\begin{array}{c}1 \\ 0\end{array}\right] \\ & \mathbf{u}_2=\left[\begin{array}{c}0 \\ 1\end{array}\right]\end{aligned}	\begin{aligned} & \mathbf{u}_1=\left[\begin{array}{c}1 \\ -i\end{array}\right] \\ & \mathbf{u}_2=\left[\begin{array}{c}1 \\ +i\end{array}\right]\end{aligned}	\mathbf{u}_1=\left[\begin{array}{l}1 \\ 0\end{array}\right]	\begin{aligned} & \mathbf{u}_1=\left[\begin{array}{l}1 \\ 1\end{array}\right] \\ & \mathbf{u}_2=\left[\begin{array}{c}1 \\ -1\end{array}\right]\end{aligned}

特征方程的推导

对于公式 (1)，移项得：

A \vec{x} - \lambda \vec{x} = \vec{0} \tag{2}

由于 \vec{x} 是一个非零向量，即 \vec{x} = E \times \vec{x} （E 为单位矩阵）因此我们可以将公式 (2) 写成：

(A - \lambda E) \vec{x} = \vec{0} \tag{3}

\vec{x} = \vec{0} 时，式子显然成立，于是我们讨论 \vec{x} \neq \vec{0} 的情况。

于是我们可以得到 |A - \lambda E| = 0，即为特征方程。

假设：

A - \lambda E = \begin{bmatrix} {a_{11} - \lambda} & {a_{12}} & \cdots & {a_{1n}} \\ {a_{21}} & {a_{22} - \lambda} & \cdots & {a_{2n}} \\ \vdots & \vdots & \ddots & \vdots \\ {a_{n1}} & {a_{n2}} & \cdots & {a_{nn} - \lambda} \end{bmatrix} = 0 \tag{4}

则可以求得最多 n 个特征值 \lambda_i ~ \{i \mid i = 1, 2, \cdots, m (m \leq n) \}。

特征值相关性质：

\lambda_1 + \lambda_2 + \cdots + \lambda_n = a_{11} + a_{22} + \cdots + a_{nn}

\lambda_1 \lambda_2 \cdots \lambda_n = |A - \lambda E|

A^2\mathbb{x} = A(A\mathbb{x}) = A(\lambda \mathbb{x}) = \lambda(A\mathbb{x}) = \lambda^2 \mathbb{x} \Rightarrow \color{FFC340}{A^kx = \lambda^k} x

特征向量求解

对于给定的特征值 \lambda_i，我们可以使用基础解系法求得对应的特征向量 \vec{x}_i。
假设：

(A - \lambda_i E) \vec{x}_i = \vec{0}

则有：

\begin{bmatrix} {a_{11} - \lambda_i} & {a_{12}} & \cdots & {a_{1n}} \\ {a_{21}} & {a_{22} - \lambda_i} & \cdots & {a_{2n}} \\ \vdots & \vdots & \ddots & \vdots \\ {a_{n1}} & {a_{n2}} & \cdots & {a_{nn} - \lambda_i} \end{bmatrix} \begin{bmatrix} {x_{i1}} \\ {x_{i2}} \\ \vdots \\ {x_{in}} \end{bmatrix} = \vec{0} \tag{5}

我们将 A - \lambda_i E 化成行最简型，然后将相应的特征向量求解出来即可。

\vec{x}_i 是 A 的特征向量，当且仅当 \vec{x}_i 是 A - \lambda_i E 的特征向量

使用python求解特征值和特征向量

python 中的 numpy.linalg.eig() 函数可以很方便地求解特征值和特征向量。

例如，对于下面的矩阵：

A = \begin{bmatrix} {3} & {1} \\ {1} & {3} \end{bmatrix}

我们可以使用以下代码进行求解：

import numpy as np

a = np.mat([[3, 1], [1, 3]])
lam, x = np.linalg.eig(a)

结果如下：

lam:       array([4., 2.])
x:         matrix([[ 0.70710678, -0.70710678],
                 [ 0.70710678,  0.70710678]])

相似矩阵

相似矩阵（Similar Matrix）是两个矩阵 A 和 B，使得它们满足 B = M^{-1}AM（其中 M 是一个可逆矩阵）。那么我们就称 B 和 A 相似。

我们可以这样理解，设 \vec{x} 是一个非零 n 维向量，设有如下式子：

B \vec{x} = \lambda \vec{x} \\ \Downarrow \\ (M^{-1} A M) \vec{x} = \lambda \vec{x}

化简可以得到：

A (M \vec{x}) = \lambda (M \vec{x}) \tag{6}

也就是说矩阵 A 和矩阵 B 具有相同的特征值 \lambda，而特征向量不一定相同。

特征值分解

对于一个 n \times n 的矩阵 A（一般情况下，矩阵 A 应该有 n 阶），可以分解成如下形式：

A = Q \Lambda Q^{-1} \tag{7}

其中 \Lambda 是 n \times n 的对角矩阵，其对角线上的元素满足以下关系（\lambda_i 是矩阵 A 的特征值）：

\Lambda_{ii} = \lambda_i ~ (\lambda_i \in \Bbb{R})

那么我们为什么可以使用式 (7) 来表示矩阵 A 呢？

对于式 (1)，我们这样理解：矩阵 A 对向量 \vec{x} 的变换效果只有拉伸，而并没有旋转。

也可以说，对于一个 n \times n 的矩阵 A，应该存在 n 个非零的特征向量使得式 (1) 成立。

对于式 (1) 的完备形式：

A(\vec{x_1}, \vec{x_2}, \cdots, \vec{x_n}) = (\lambda_1 \vec{x_1}, \lambda_2 \vec{x_2}, \cdots, \lambda_n \vec{x_n}) = (\vec{x_1}, \vec{x_2}, \cdots, \vec{x_n}) \begin{bmatrix} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_n \end{bmatrix} \tag{8}

可以得到如下式子：

A Q = Q \Lambda

也就是可以转化成式 (7) 的形式。

SVD奇异值分解

奇异值分解(Singular Value Decomposition，SVD) 是在机器学习领域广泛应用的算法，它不光可以用于降维算法中的特征分解，还可以用于推荐系统，以及自然语言处理等领域。

为什么使用奇异值分解算法？

(1) 特征值分解仅适用于提取方阵特征，但实际场景应用中大部分数据都不是方阵；

(2) 数据可能是有许多 “0” 值的稀疏矩阵，因此我们需要提取主要特征值。

(3) 奇异值分解可以将复杂的矩阵分解成简单的子矩阵，通过子矩阵来描述复杂矩阵的特性。

预备知识

对于一个 m \times n 矩阵 A 来说，A^T 是矩阵 A 的转置矩阵，A^H 是矩阵 A 的共轭转置矩阵²。

其中，A^H 有以下定义：

共轭转置是在转置的基础上，对复数矩阵中的每一个元素取复共轭。
对于实数矩阵，共轭转置矩阵与原矩阵相同。
对于复数矩阵，共轭转置矩阵会将矩阵中的元素取复共轭，然后对行列进行转置。

若一个矩阵 A 满足 A^H A = A A^H = I（I 为单位矩阵），那么我们称矩阵 A 为酉矩阵（幺正矩阵）。若矩阵 A 是定义在实数域中，那么酉矩阵就叫实正交矩阵。

酉矩阵性质：
(1) A^H A = A A^H = E；
(2) A^H = A^{-1}；
(3) |det A| = 1；
(4) 对于任意向量 x，有\Vert Ax \Vert_2 = \Vert x \Vert_2.

奇异值定义

对于一个 m \times n 的矩阵 A，我们设 rank(A) = r，A^H A 的特征值为 \lambda_1, \lambda_2, \cdots, \lambda_n (\lambda_k = 0, k > r)，则矩阵 A 的奇异值定义为：

\sigma_i = \sqrt{\lambda_i} ~ (\lambda_i = 1, 2, \cdots, n)

A=U \begin{bmatrix} \sigma_1 & 0 & \cdots & 0 \\ 0 & \sigma_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \sigma_n \end{bmatrix} V^H \tag{9}

其中，\lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_n \geq 0，U 和 V 都是酉矩阵，即满足 U^T U = V^T V = E.

那么为什么要大费周章使用 A^H A 的特征值来定义奇异值呢？

对于实数矩阵 A_{m \times n}，我们不能直接求它的特征值，但对于 A^T A 和 A A^T，分别为 n 阶和 m 阶对称方阵。他们的秩 R(A^T A) = R(A A^T) = R(A)，且两个对称矩阵的非零特征值相同，这两个对称矩阵的特征值矩阵是正交矩阵，特征值均为正实数，因此可以得到如下关系：特征值的平方根 = 奇异值。

奇异值分解公式推导

SVD 的核心就是找到一组 A 的行空间中正交基 v_1, v_2, \cdots, v_n，使得：

A \begin{bmatrix} v_1 & v_2 & \cdots & v_n \end{bmatrix} = \begin{bmatrix} \sigma_1 u_1 & \sigma_2 u_2 & \cdots & \sigma_n u_n \end{bmatrix} = \begin{bmatrix} \mathbb{u_1, u_2, \cdots, u_n} \end{bmatrix} \begin{bmatrix} \sigma_1 & & & \\ & \sigma_2 & & \\ & & \ddots & & \\ & & & \sigma_n \end{bmatrix} \tag{10}

其中 u_1, u_2, \cdots, u_n 是一组在 A 的列空间中的正交基。写成矩阵形式：AV = U\Sigma。实际上特征值分解是SVD的一个特例。

将矩阵同时右乘 V^{-1} 可以得到式 (9)，即 A = U \Sigma V^T。

接下来我们将对于如何计算奇异值分解进行讨论。

如果我们将 A^T 和 A 做矩阵乘法，那么会得到一个 n \times n 的方阵 A^T A，以及一个 m \times m 的方阵 A A^T。

那么我们将其进行特征值分解：

(A^T A) \vec{v_i} = \lambda_i \vec{v_i} \\ (A A^T) \vec{u_i} = \lambda_i \vec{u_i}

可以求出相应的特征值和特征向量。

将所有的特征向量 v_i 合并成 n \times n 的矩阵 V，将所有的特征向量 u_i 合并成 m \times m 的矩阵 U，即：

(\vec{v_1}, \vec{v_2}, \cdots, \vec{v_n}) = V \\ (\vec{u_1}, \vec{u_2}, \cdots, \vec{u_m}) = U

一般我们将矩阵 V 中的每个特征向量叫做矩阵 A 的右奇异向量，将矩阵 U 中的每个特征向量叫做矩阵 A 的左奇异向量。（其实就是式 (9) 中的相对位置）

接下来我们将对奇异值矩阵 \Sigma 进行相应求解。

我们将式 (9) 同时左乘一个 A^T 则:

A^T A = (U \Sigma V^T)^T U \Sigma V^T = V \Sigma^T U^T U \Sigma V^T \tag{11}

由于矩阵 U 和 V 都是酉矩阵，并且矩阵 \Sigma 是对角阵，所以：

A^T A = V \Sigma^2 V^{-1} \tag{12}

同理，我们可以求出：

A A^T = U \Sigma^2 U^{-1} \tag{13}

我们可以发现此时满足 “A = Q \Lambda Q^{-1}” 的形式，即特征值分解。由于 A A^T（或 A^T A）的特征值为：

\Lambda = \begin{bmatrix} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_n \end{bmatrix}

于是可以得到以下等价式子：

\Lambda = \Sigma^2 \Longleftrightarrow \lambda_i = \sigma_i^2

使用python进行奇异值分解

使用 numpy库中的 numpy.linalg.svd()函数可以很方便的求解特征值和特征向量。

例如，对于下面的矩阵：

A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}

我们可以使用以下代码进行求解：

import numpy as np
A = np.array([[1, 2], [3, 4]])
U, s, V = np.linalg.svd(A)

运行结果如下：

U:         matrix([[-0.40455358, -0.9145143 ],
                 [-0.9145143 ,  0.40455358]])
s:         array([5.4649857, 0.36596619])
V:         matrix([[-0.57604844, -0.81741556],
                 [ 0.81741556, -0.57604844]])

实际运用

SVD 主要用于降维，即把一个高维度的矩阵通过某种方式映射到低维度的矩阵。

在分解成 U, \Sigma, V 之后，由于 \Sigma 是单调递减的，也就是说越往后权值越小，于是我们可以选择其中的一部分，而舍弃掉权值较小的那些特征值，达到降维的效果。

以下是使用 SVD 进行图片压缩的例子：

这是压缩前的图片：

Dog（540KB）

这是压缩后的图片：

Dog（258KB）

SVD分解结果如下：

Result